Let
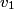 and and 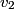 denote the speeds of the first and the second blocks, respectively, after the collision. We are given that denote the speeds of the first and the second blocks, respectively, after the collision. We are given that 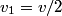 and we would like to find and we would like to find 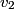 . In elastic collisions, kinetic energy is conserved. The initial kinetic energy is . In elastic collisions, kinetic energy is conserved. The initial kinetic energy is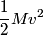 The final kinetic energy is 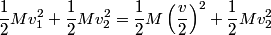 Setting the initial kinetic energy equal to the final kinetic energy gives 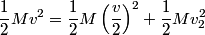 Dividing both sides by  simplies this equation to simplies this equation to 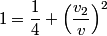 Solving for 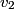 gives gives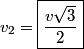 Therefore, answer (C) is correct. |